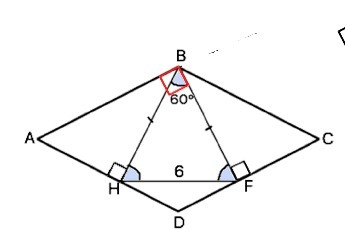
Высоты ромба равны.
В ∆ HBF стороны ВН=BF. ⇒ этот треугольник равнобедренный.
Т.к. угол HBF=60°, углы при его основании HF также равны 60°.⇒
∆ HBF - равносторонний. ВН=ВF=6 см.
Высоты ромба перпендикулярны обеим его противоположным сторонам. ⇒
∠АВF=90°. Поэтому ∠АВН=90°-60°=30°
Все стороны ромба равны.
АВ=ВН:cos30°
АВ=6:(√3/2)=4√3
Одна из формул площади ромба
S=h•a⇒
S=6•4√3=24√3 см²