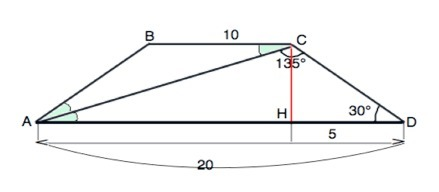
В трапеции основания параллельны, СD- секущая, ⇒ сумма внутренних односторонних углов рана 180°.
Угол ВСА=180°-135°-30°=15°
Угол САD=углу ВСА как накрестлежащий.
Следовательно, угол ВАС=30°-15°=15° ⇒ АС - биссектриса.
В ∆ АВС углы при основании равны - ∆ АВС равнобедренный, и АВ=ВС=10 см
Трапеция равнобедренная, СD=АВ=10 см.
Периметр АВС=10+10+10+20=50 см
--------------------
НО!Высота равнобедренной трапеции, опущенная на большее основание, делит его на отрезки, меньший из которых равен полуразности оснований.
HD=(AD-BC):2=5 см
Тогда в ∆ CHD гипотенуза CD=АВ=DH:cos30°=10/√3
И тогда периметр будет 30+20/√3 (?!)
Получилась нестыковка: Не могут одни и те же стороны трапеции иметь два различных значения.
Эта задача не единственная с таким же условием, значит, напутали не авторы вопроса, а составители задачи. Что. к сожалению, не так уж редко бывает.
* * *
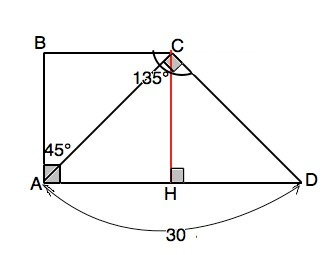
2)
Основания трапеции параллельны, АВ - секущая, поэтому ∠АВС=∠ВАD=90°
Поскольку ∠ВАС=45°, то и ∠ВСА=45°, ⇒треугольник АВС равнобедренный.
В треугольнике АСD угол СDA=180°-135°=45°.
∠САD=∠BAD-∠BAC=45°
Значит, ∆ АСD- равнобедренный.
Тогда его высота к гипотенузе является и медианой и равна половине её длины.
СН=30:2=15 см
Кратчайшее расстояние между двумя параллельными прямыми - перпендикуляр. Поэтому меньшей боковой стороной является сторона АВ. Высота СН - тоже перпендикуляр. поэтому АВ=СН=15 см