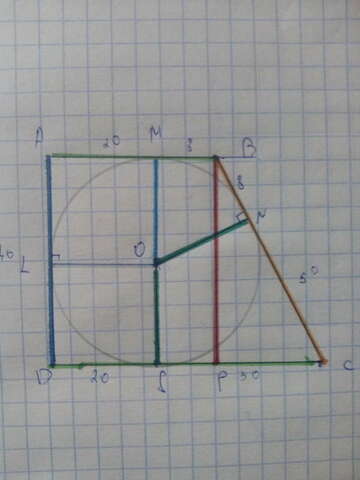
Пусть BP ⊥ DC.
Тогда BP||MS и MP = MS (MS ⊥ AB, MBPS - прямоугольник).
MS = 2R = 2•20 см = 40 см.
Тогда BP = 40 см.
BC = BN + NC = 8 см + 50 см = 58 см.
По теореме Пифагора:
PC = √BC² - BP² = √58² - 40² = √3364 - 1600 = √1764 = 42 см.
SP = MB - по свойству сторон прямоугольника
MB = BN - как отрезки касательных, проведённые из одной точки.
Тогда SP = MB = 8 см.
SC = 8 см + 42 см = 50 см.
ADSM - прямоугольник => AM = DS и AD = MS - по свойству сторон прямоугольника.
Тогда AD = 2R = 40 см..
AL = LD, т.к. AMOL и LOSD - квадраты (все углы равны по 90° и смежные стороны MO и OL, OS и LO равны как радиусы). (1)
Тогда AL = 1/2AD = 20 см.
AL = AM = DS = 20 см.
AB = AM + MB = 20 см + 8 см = 28 см.
DC = 20 см + 50 см = 70 см.
PABCD = 28 см + 58 см + 70 см + 40 см = 196 см.
2) BN = MB = 8 см
AM = AL = LD = DS = R = 20 см (из условия (1))
NC = SC = 50 см
PABCD = AB + BC + CD + DC = 20 см + 8 см + 8 см + 50 см + 50 см + 20 см + 20 см + 20 см + 20 см = 196 см.
Ответ: 196 см.