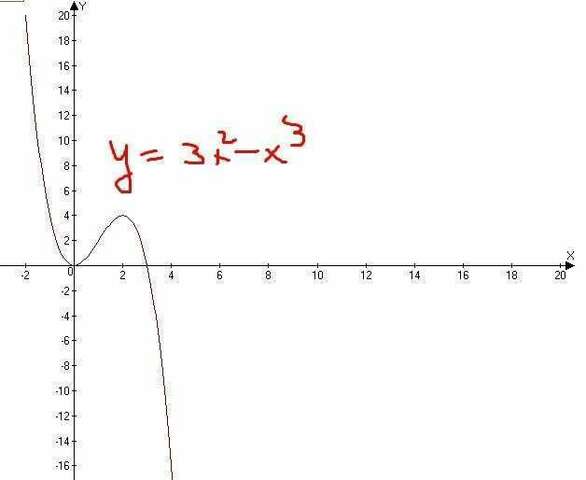
Первый рисунок.

1. область визначення функції:

2. Дослідимо на непарність функції.


функція ні парна ні непарна.
3. Функція не періодична.
4. Точки перетину з віссю Ох і Оу.
4.1. З віссю Ох:

4.2. Точки перетину з віссю Оу.

5. Точки екстремуми.


- точки екстремуму.
__-__(0)___+___(2)__-___
Функція спадає на проміжку

i

, а зростає на проміжку -

. В точці

функція має точку локального мінімуму, а в точці

- локального максимуму.
6. Точки перегину.

Горизонтальних, вертикальних і похилих асимптот немає.
5. Похідна від шляху є швидкість, тобто:

швидкість стане нульовою, якщо


6. рівняння дотичної має вигляд:

Похідна функції:

Знайдемо значення похідної в точці


Знайдемо значення функції в точці


Тоді рівняння дотичної буде мати вигляд: