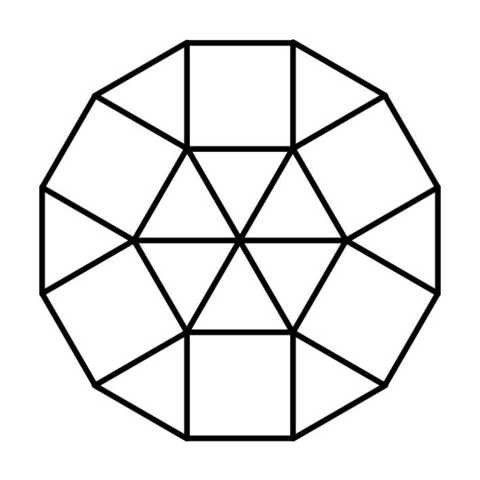
Не буду рассказывать, как я до этого доходил, но доказывается построением, как и всегда, когда хочется доказать существование.
Берем правильный 12-ти угольник, внешнее кольцо выкладываем из чередующихся квадратов и треугольников (сумма их углов при вершинах равна 150, как раз углу правильного 12-ти угольника). Оставшийся внутренний правильный шестиугольник выкладываем треугольниками.
Смотри приложение