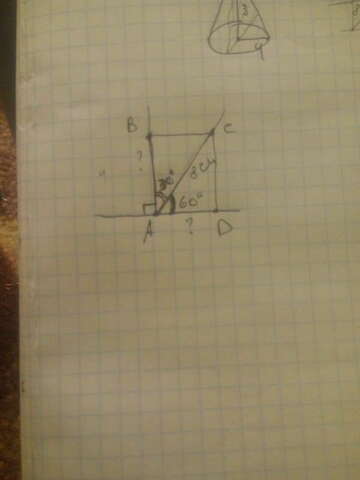
Проведём отрезок из точки В в точку С под прямым углом.
угол САD=90-60=30°
сторона лежащая против угла в 30° равна половине гипатенузы, следовательно ВС=8/2=4(см)
теперь по теореме Пифагора(т.к. мы сделали прямоугольный треугольник)
АС²=АВ²+ВС²
сейчас выражаем катет АВ из данной формулы:
АВ²=АС²-ВС²
АВ²=8²-4²=64-16=48
АВ=√48=4√3(см)
проведём также отрезок СD к плоскости под прямым углом, и получим прямоугольник ABCD, где все углы равны 90°, и по свойствам прямоугольников противолежащие стороны равны, ВС=AD=4(см)
Ответ:длина перпендикуляра АВ= 4√3 см, а длина проекции АD=4 см.
(фото чертежа прикрепил)