Определение: Прямая пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
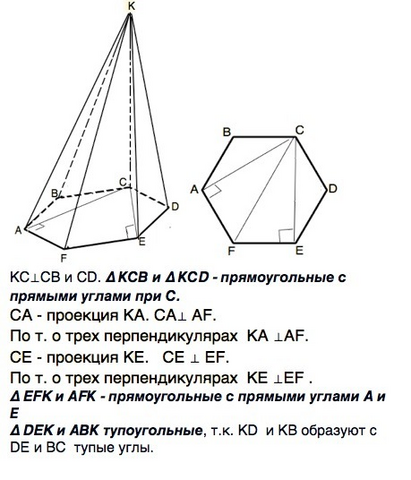
Следовательно, КС⊥СВ и CD. Углы КСВ и КСD- прямые, и ∆ КСВ и ∆ КСD - прямоугольные с прямыми углами при С.
Проекции наклонных КЕ и КА перпендикулярны соответственно сторонам EF и AF шестиугольника.
По т. о трех перпендикулярах КА ⊥ AF, а СЕ перпендикулярна EF. ⇒
∆ EFK и АFК - прямоугольные с прямыми углами А и Е.
∆ DEK и АВК тупоугольные, т.к. КD и КВ образуют с DE и ВС тупые углы.