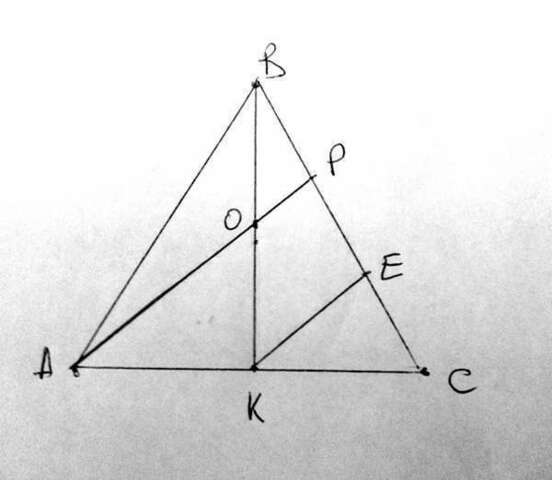
Проведем из точки К отрезок КЕ параллельный АР до пересечения со стороной ВС.
Треугольники АРС и КЕС подобны по двум углам, т.к. угол А общий, Поскольку в равнобедренном треугольнике АВС высота ВК является его медианой, то АК=СК и СК=(1/2)*АС.
Как следствие, коэффициент подобия треугольников СКЕ и САР равен 1/2.
Поэтому СЕ=(1/2)*СР, СЕ=РЕ.
С учетом того, что ВР/РС=1/2, СЕ=РЕ=ВР.
Треугольники ВКЕ и ВОР подобны по двум углам: угол КВЕ общий, Коэффициент подобия этих треугольников 1/2, т.к. ВР=РЕ, ВР=(1/2)*ВЕ.
Из подобия треугольников следует, что ВО=(1/2)*ВК, что и требовалось доказать.