Помогите пожалуйста решить задачу по геометрии с обьяснениями За помощь даю 40 баллов! ...

Question

Помогите пожалуйста решить задачу по геометрии с обьяснениями
За помощь даю 40 баллов!
Помогите пожалуйста решить задачу, очень нужно
Отрезок KM является диаметром окружности, а точка L принадлежит окружности. Расстояния от точек K и M к касательной, проведенной в точке L, равни 4 и 20 см соотвественно. Найдите радиус окружности

Answer 1

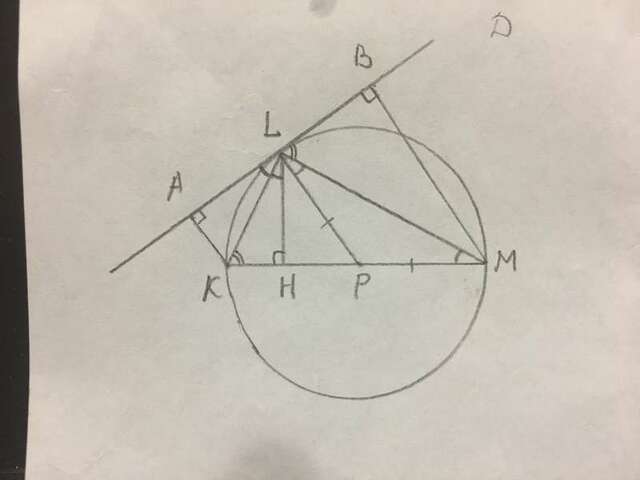
Треугольник LKM прямоугольный т.к. КМ  диаметр окружности.
КА=4 см, МВ=20 см.
КМ=?

Проведём высоту LН и медиану LP. LP - радиус. LP⊥AB. 
Тр-ник LРМ равнобедренный, значит ∠MLP=∠LMP.
∠MLB=∠РLB-∠MLP=90-∠LMK=∠LKM.
Тр-ки LMH и LMВ равны по углам и общей гипотенузе, значит МН=МВ=20 см.

Треугольники LKM и LKH подобны, значит ∠LMK=∠KLH.
∠HLP=∠KLM-∠KLH-∠MLP=90-2∠LMK.
∠ALK=∠ALP-∠HLP-KLH=90-(90-2∠LKM)-∠LKM=∠LKM.
Треугольники ALK и KLH равны по углам и общей гипотенузе, значит КН=АК=4 см.

Итак, КМ=КН+МН=4+20=24 см - это ответ.

---