Решение:
Сперва определим ОДЗ неравенства. Очевидно, что значение x не должно совпадать со значением 2.
Поскольку, знаменатель - это неотрицательное число, то числитель тоже не должен быть отрицательным.
Решается методом интервалов. В силу того, что сама дробь должна быть больше 0, то числитель тоже должен быть больше 0 (про знаменатель уже сказали). Как решать неравенство методом интервалов? На вашем примере, думаю, будет все ясно.
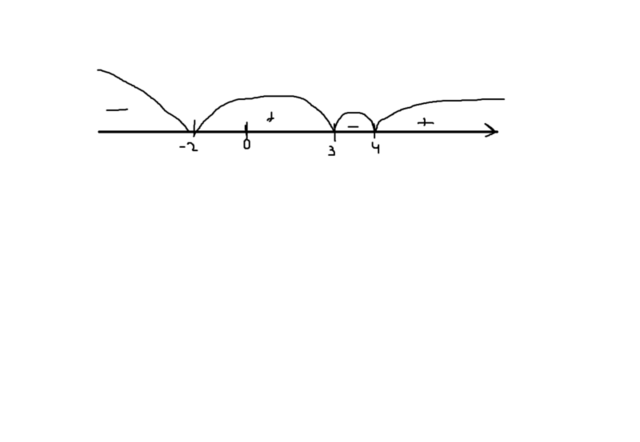
Находим нули функций (иными словами, находим те значения x, так, чтобы функция была равна 0 и соблюдалось ОДЗ). Это: x=-2;3;4. Отмечаем значения на числовом луче. Определяем знакопостоянство: если x<-2, то числитель отрицателен (отмечаем на луче). При всех остальных значениях числитель - положительный (за исключением x=2, потому что при этом значении знаменатель обращается в нуль, а мы знаем,что на 0 делить нельзя). Получили интервал: отрицательный: <img src="https://tex.z-dn.net/?f=%28-%5Cinfty%3B-2%29" id="TexFormula2" title="(-\infty;-2)" alt="(-\infty;-2)" align="absmiddle" class="latex-formula">
И положительный:  (рис. 2)
(рис. 2)
Далее, снова отрицательный: 
И положительный: 
Но, в условии сказано: найти кол-во целых отрицательных чисел, удовлетворяющих неравенству. Опять же, обращаясь к нашему промежутку чисел, находим, что их только 2: -2 и -1. Однако, -2 обращает дробь в 0, поэтому, число только одно.
Ответ: -1