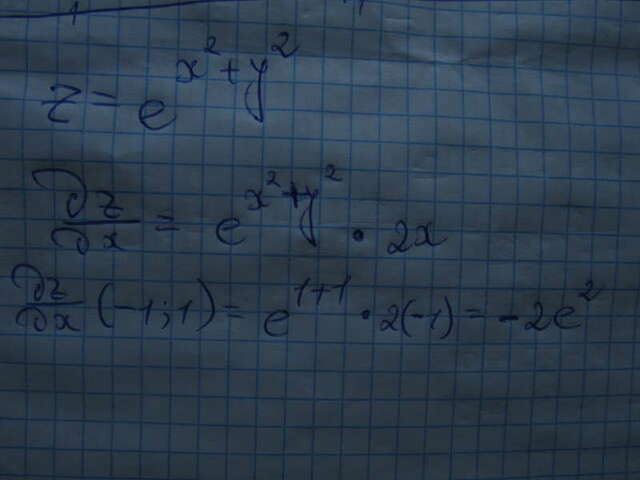Частная производная функции z=e^(x^2+y^2) по переменной x в точке М (-1;1) равна?...

Question

Частная производная функции z=e^(x^2+y^2) по переменной x в точке М (-1;1) равна?

Желательно подробно.

Answer 1

Решение на фото.

При дифференцировании следуем правилу дифференцированию сложной функции: производная экспоненты — сама экспонента, после чего нужно умножить на производную показателя (x^2+y^2) по х, а это будет 2х.

Далее просто подставляем имеющиеся значения х и у.

---

Comments

Можешь по подробнее рассказать от куда 2x взялся, понять не могу.

---

При дифференцировании (x^2+y^2) по х мы дифференцируем отдельно каждое слагаемое. Производная x^2 равна 2x (табличное значение), а вот производная y^2 будет равна нулю, так как дифференцирование по иксу (в этом случае y^2 считается просто константой).

---

Все теперь понял. Спасибо.