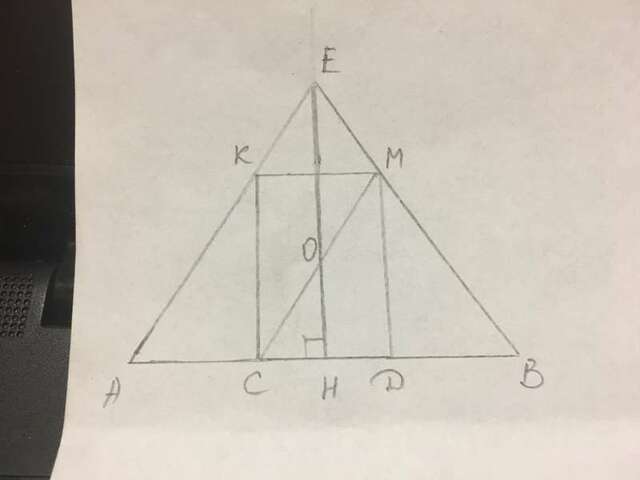
На рисунке показано осевое сечение конуса и цилиндра.
R=АН=5, АЕ║СМ, СМ=26/3, h=МД=8.
АЕ=?.
В прямоугольном тр-ке СМД СД²=СМ²-МД²=(26/3)²-8²=100/9,
СД=10/3.
СД - диаметр цилиндра. Его радиус: r=СН=СД/2=5/3.
Треугольники СМД и СОН подобны, т.к. оба прямоугольные и ∠МСД - общий. СН=СД/2 ⇒ СО=СМ/2=13/3.
Прямоугольные треугольники АЕН и СОН подобны, т.к. ∠ЕАН=ОСН при параллельных АЕ и СМ и секущей АВ, значит АЕ/СО=АН/СН,
АЕ=АН·СО/СН=5·(13/3):(5/3)=5·13/5=13 - это ответ.