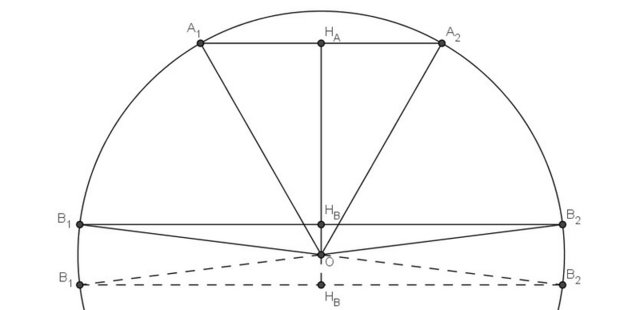
Проводим радиусы в концы хорд.
Рассмотрим треугольник OA₁A₂. Он равнобедренный, так как OA₁ = OA₂ = R = √65. Пусть OHₐ - высота, проведённая к основанию равнобедренного треугольника, тогда она и медиана, HₐA₂ = A₁A₂ / 2 = 4.
Рассмотрим треугольник OHₐA₂. Он по построению прямоугольный, по теореме Пифагора OHₐ = √(R² - HₐA₂²) = √(65 - 16) = 7.
Пусть OHₐ пересекает вторую хорду в точке Hb. Так как A₁A₂ || B₁B₂, то OHb ⊥ B₁B₂.
Аналогично OHb =√(65 - 64) = 1.
Расстояние между перпендикулярными прямыми измеряется по перпендикуляру HₐHb. В зависимости от того, лежат хорды по одну сторону от диаметра или по разные, возможны два ответа: 7 + 1 = 8 или 7 - 1 = 6.
Ответ. 6 или 8.