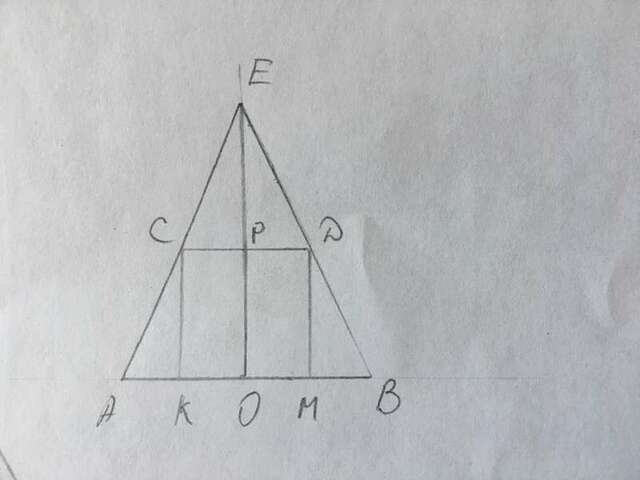Верхнее основание призмы - прямоугольный треугольник - касается своими вершинами боковой поверхности конуса. Плоскость верхнего основания пересекает конус по окружности, диаметром которой является гипотенуза треугольника основания. Значит можно нарисовать осевое сечение конуса в котором ЕО - его высота, ЕО=10, АВ=2R=2·5=10, СД - гипотенуза основания призмы, СК - высота призмы, СД=СК.
СД║АВ, значит тр-ки АЕВ и СЕД подобны.
Пусть СК=СД=х, тогда ЕР=ЕО-РО=10-х.
Исходя из подобия, СД/АВ=ЕР/ЕО,
х/10=(10-х)/10,
10х=100-10х,
20х=100,
х=5.
Гипотенуза основания и высота призмы равны 5.
Второй катет основания: b²=c²-a²=5²-4²=9, b=3.
Площадь основания призмы: S=ab/2=3·4/2=6.
Объём призмы: V=Sh=6·5=30 (ед²) - это ответ.