В остроугольном треугольнике ABC проведена из вершины B высота, которая продолжена до...

Question

В остроугольном треугольнике ABC проведена из вершины B высота, которая продолжена до пересечения с описанной окружностью в точке E, причем AE=4. Высота AD = 9, а сторона BC = 18. Найти отрезки, но которые точка D делит сторону BVC.

Comments

Прошу прощения, в конце надо читать "сторону BC"

Answer 1

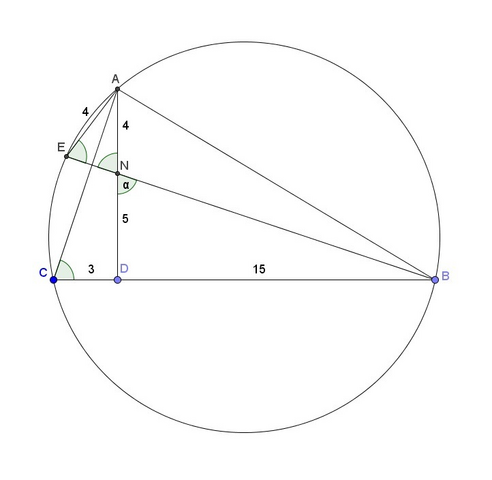
Пусть BE∩AD=N. Тогда ∠AEB=∠ACB=∠ANE=α по свойствам вписанных и прямых углов. Т.е. треугольник ANE - равнобедренный, т.е. AN=AE=4, откуда ND=9-4=5. Также tg(α)=BD/5=9/DC и BD+DC=18. Т.е. BD·DC=45, а значит BD и DC - корни уравнения x²-18x+45=0, т.е. равны 3 и 15.

В картинке приложен вариант чертежа с DС=3 и BD=15. Второй вариант получится, когда ∠C<∠B и, соответственно, будет DC=15 и BD=3.<hr>

Comments

Все замечательно. Единственно я чуть-чуть по-другому стал бы искать произведение BD на DC: если продолжить AD до пересечения с описанной окружностью в точке K, то DK=DN=5, поэтому BD*DC=AD*DK=9*5=45.