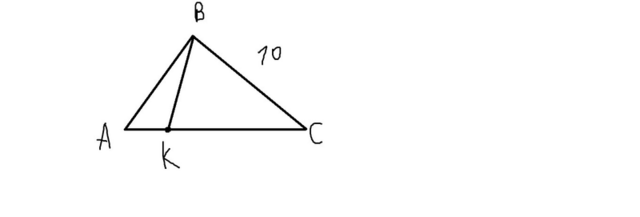
Начнем с площадей. По условию, S abk / S kbc = 1 / 3. Выразив из искомого соотношения S kbc, получаем: S kbc = 3 * S abk. Распишем площади треугольников: S abk = 1/2 * BK * AK * sin(∠BKA). S kbc = 1/2 * BK * KC * sin(∠BKC). Получаем: 1/2 * BK * KC * sin(∠BKC) = 3 * 1/2 * BK * AK * sin(∠BKA). Синусы смежных углов BKC и BKA равны по определению, разделим обе части на 1/2 * BK. Получаем: KC = 3 * AK. Теперь перейдем ко второму соотношению: BC / AC = AK / KC. BC = 10, AC = AK+KC. Получаем: 10 / (AK+KC) = AK/KC. Подставив KC =3 * AK, получается: 10 / (AK+3 * AK) = AK / (3 * AK) , 10 / (4 * AK) = 1 / 3. Отсюда 4 * AK = 30, AK = 15 / 2. Тогда KC = 3 * (15/2) = 45/2. AC=AK+KC=(15/2)+(45/2)=60/2=30. Ответ: 30