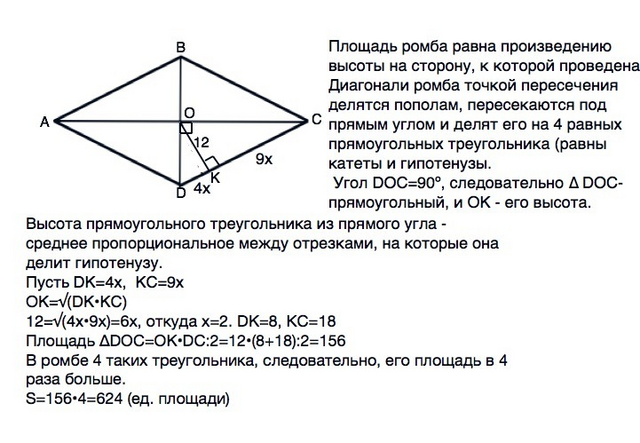
Площадь ромба равна произведению высоты на сторону, к которой проведена.
Диагонали ромба точкой пересечения делятся пополам, пересекаются под прямым углом и делят ромб на 4 равных прямоугольных треугольника ( т.к. равны ихкатеты и гипотенузы).
Угол DOC=90º, следовательно ∆ DOC- прямоугольный, и ОК - его высота.
Высота прямоугольного треугольника из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
Пусть DК=4x, KC=9x
ОК=√(DK•KC)
12=√(4х•9x)=6х, откуда х=2.⇒ DK=2•4=8, КС=2•9=18
Площадь ∆DOC=OK•DC:2=12•(8+18):2=156
В ромбе 4 таких треугольника, следовательно, его площадь в 4 раза больше.
S=156•4=624 (ед. площади)
-------- или:
Высота ромба равна 2•OK=24. S=24•26=624 (ед. площади)