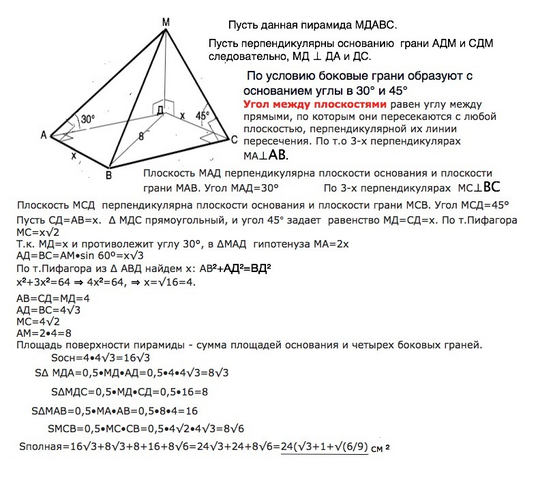
Обозначим вершины пирамиды МДАВС.
Пусть перпендикулярны основанию грани АДМ и СДМ следовательно, МД ⊥ ДА и ДС.
По условию боковые грани образуют с основанием углы в 30° и 45°
Угол между плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
По т.о 3-х перпендикулярах МА⊥АВ. Плоскость МАД⊥ плоскости основания и плоскости грани МАВ. ∠ МАД=30°
По т. о 3-х перпендикулярах МС⊥ВС. Плоскость МСД ⊥плоскости основания и плоскости грани МСВ. ∠ МСД=45°
Примем СД=АВ=х. ∆ МДС прямоугольный, и угол 45° задает равенство МД=СД=х. По т.Пифагора МС=х√2
Т.к. МД=х и противолежит углу 30°, в ∆МАД гипотенуза МА=2х
АД=ВС=АМ•sin 60º=x√3
По т.Пифагора из ∆ АВД найдем х: АВ²+АД²=ВД²
х²+3х²=64 ⇒ 4х²=64, ⇒ х=√16=4.
АВ=СД=МД=4
АД=ВС=4√3
МС=4√2
АМ=2•4=8
Площадь поверхности пирамиды равна сумме площадей основания и четырех её боковых граней.
Sосн=4•4√3=16√3
S∆ МДА=0,5•МД•АД=0,5•4•4√3=8√3
S∆МДС=0,5•МД•СД=0,5•16=8
S∆MAB=0,5•MA•AB=0,5•8•4=16
S∆MCB=0,5•MC•CB=0,5•4√2•4√3=8√6
Sполная=16√3+8√3+8+16+8√6=24√3+24+8√6=24(√3+1+√(6/9) см²