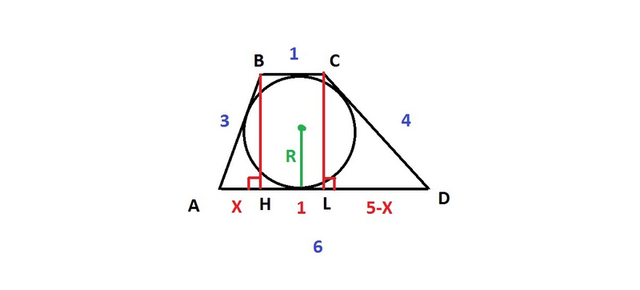
Радиус окружности, вписанной в трапецию, равен половине высоты этой трапеции. (диаметр окружности d равен высоте трапеции)
Если в трапецию вписана окружность, значит сумма противоположных сторон этой трапеции равна.
То есть ВС+AD=AB+CD
1+6=AB+4 ⇒ AB=3
проведем две высоты: ВН и CL
BCLH - прямоугольник, значит BC=HL=1
Если AD=6, то AH+LD=AD-HL=6-1=5
Пусть AH=x, тогда LD=5-x
ВН = CL=h -высоты
Рассмотрим ΔABH и ΔCDL - они прямоугольные, значит для них действует теорема Пифагора
BH²=AB²-AH²
h²=3²-x²
CL²=CD²-LD²
h²=4²-(5-x)²
составляем систему:

левые части равны, значит приравниваем правые:
9-х²=16-(5-x)²
9-х²=16-25+10х-х²
10х=18
х=1,8
h²=9-x²=9-1.8²=5.76
h=√5.76=2.4
d=h=2.4
C=2πR=πd=2.4π≈2.4*3.14=7.536
ОТВЕТ: 2,4π или ≈7.536