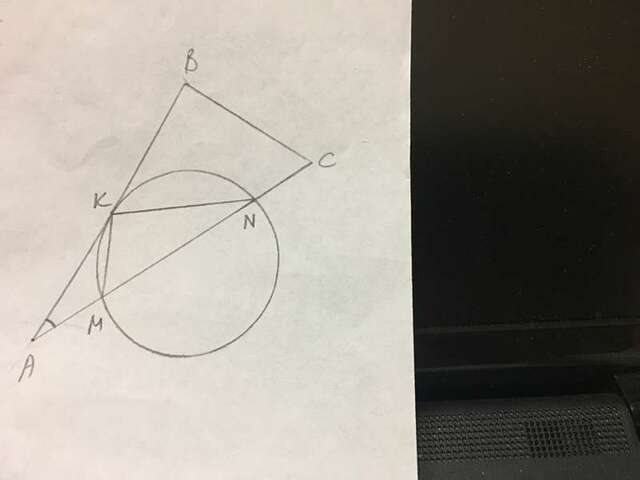
АМ=16, АN=39, cos∠BAC=√39/8, K∈AB.
R=?
По теореме о касательной и секущей АМ·АN=AK² ⇒ AK=√(AM·AN)=√(16·39)=4√39.
В тр-ке АKN по теореме косинусов:
KN²=AN²+AK²-2AN·AK·cosA=39²+16·39-2·39·4√39·√39/8=16·39,
KN=4√39.
AK=KN, значит тр-ник АКN - равнобедренный. ∠KAN=∠KNA.
AM·AN=AK² ⇒ AK/AN=AM/AK C таким отношением сторон треугольники AKN и АКМ подобны, следовательно тр-ник АКМ равнобедренный. АК=АМ=16.
В тр-ке КМN по теореме синусов КМ/sinN=2R ⇒ R=KM/2sinN.
sin²N=1-cos²N=1-39/64=25/64.
sinN=5/8.
R=16·8/(2·5)=12.8 - это ответ.