Две окружности пересекаются в точках C и D. точка B центр второй окружности, а отрезок...

Question

Две окружности пересекаются в точках C и D. точка B центр второй окружности, а отрезок AB- диаметр первой. из точки C провели касательную к первой окружности, которая пересекает вторую окружность в точке E , отличной от C. найдите радиус первой если радиус второй 15 а дина отрезка CE- 18

Answer 1

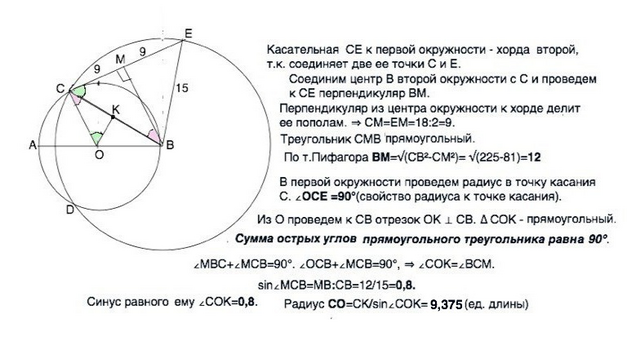
Касательная  СЕ к первой окружности - хорда  второй, т.к. соединяет две ее точки С и Е. 

Соединим центр В второй окружности с С и проведем к СЕ перпендикуляр ВМ. 

Перпендикуляр из центра окружности к хорде делит ее пополам. ⇒ СМ=ЕМ=18:2=9. Треугольник СМВ прямоугольный.     

По т.Пифагора ВМ=√(СВ²-СМ²)= √(225-81)=12 

В первой окружности проведем радиус в точку касания С. ∠ОСЕ =90°(свойство радиуса к точке касания). 

Из О проведем к СВ отрезок ОК ⊥ СВ. ∆ СОК - прямоугольный.  Сумма острых углов прямоугольного треугольника равны 90°. 

∠МВС+∠МСВ=90°. ∠ОСВ+∠МСВ=90°, ⇒ ∠СОК=∠ВСМ.  sin∠МСВ=МВ:СВ=12/15=0,8.  Синус равного ему ∠СОК=0,8. 

Радиус СО=СК/sin∠COK= 9,375 (ед. длины)

---