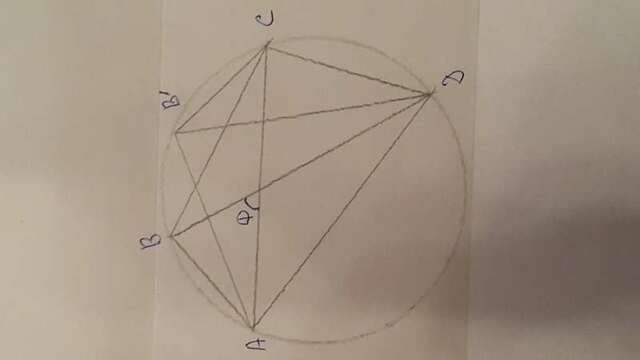
Строго говоря, теорема Птолемея дает необходимое и достаточное условие того, что около четырехугольника можно описать окружность. Но если честно, я ни разу не встречал задачу, в которой пришлось бы использовать достаточность. То есть всегда бывает дано, что четырехугольник вписан в окружность, и отсюда делается соответствующий вывод. Предлагаю в таком виде теорему и формулировать.
Теорема Птолемея. Если четырехугольник ABCD вписан в окружность, то произведение диагоналей равно сумме произведений противоположных сторон
AC·BD=AB·CD+AD·BC.
Меня всегда удивлял тот факт, что в этой теореме приходится перемножать противоположные стороны. Как-то далеко друг от друга они расположены. Вот если бы соседние перемножались, то никакого предубеждения у меня не возникало бы. Это и дало толчок к моему доказательству.
Найдем площадь ABCD двумя способами.
Во-первых, эта площадь равна половине произведения диагоналей на синус угла между ними - эта формула, как мне кажется, школьникам должна быть известна.
Доказывается она либо разбиением четырехугольника диагоналями на 4 треугольника, либо более красиво - рассматривая его как половину (по площади) параллелограмма, чьи стороны параллельны диагоналям четырехугольника и проходят через его вершины,
Если обозначить угол между диагоналями буквой Ф, то
S=(1/2)AC·BD·sin Ф
Угол Ф - это угол между хордами AC и BD, а он, как известно из школьной программы, равен полусумме дуг AB и CD, высекаемых этими хордами. Через вписанные углы он выражается в виде суммы углов BCA и CBD. Запомним это.
Во-вторых, более или менее естественно попробовать сосчитать площадь ABCD как сумму площадей двух треугольников, скажем ABC и ADC, но в этом случае мы будем получать произведения соседних сторон, а не противоположных. Выйдем из положения не совсем обычным способом. Отрежем от четырехугольника треугольник ABC (останется нетронутым треугольник ADC) , перевернем ABC другой стороной и "приклеим" на старое место. Если Вы не любите "играть в бирюльки" и хотите "математическое рассуждение", то вот оно. Рассмотрите диаметр окружности, перпендикулярный AC, и рассмотрите точку B', симметричную точке B относительно этого диаметра. Конечно, она снова лежит на окружности, при этом AB=CB'; BC=B'A. Иными словами, мы получили четырехугольник AB'CD, площадь которого равна площади старого, с теми же сторонами, но теперь те стороны, которые были противоположными, стали соседними. Разобьем четырехугольник AB'CD на два треугольника так, чтобы их сторонами были бывшие противоположные. Тогда
S_(ABCD)=S_(AB'CD)=S_(AB'D)+S_(B'CD)=
(1/2)AB'·ADsin DAB'+(1/2)B'C·CDsin B'CD
Во вписанном четырехугольнике, как известно, сумма противоположных углов равна 180°, значит синусы этих углов равны, поэтому
S_(ABCD)=(1/2)(AB'·AD+B'C·CD)sin DAB'=
(1/2)(BC·AD+AB·CD)sin (DAC+CAB')=
(1/2)(BC·AD+AB·CD)sin (DBC+BCA)=
(1/2)(BC·AD+AB·CD)sin Ф
(углы DAC и DBC опираются на одну дугу и поэтому равны,
углы CAB' и BCA опираются на равные хорды B'C и AB и поэтому равны).
Сравнив две полученные формулы для площади ABCD, получаем искомую формулу.
Пример на использование теоремы Птолемея.
Четырехугольник ABCD вписан в окружность, AB=1, AC=2, AD=6/5, ∠ADC=90°. Найти BD.
Решение. ∠ADC=90°⇒∠ABC=90°, то есть ABCD разбит диагональю AC на два прямоугольных треугольника. С помощью теоремы Пифагора находим неизвестные катеты этих треугольников: BC=√3; CD=8/5.
По теореме Птолемея BD·AC=AB·CD+BC·AD;
2BD=8/5+6√3/5; BD=(4+3√3)/5
Заканчивая сей опус, хочу извиниться за то, что не способен сейчас сделать чертеж - очень много дел запланировано на этот вечер. Если кто-нибудь сделает мне его - отдам все заработанные на этой задаче баллы.)))