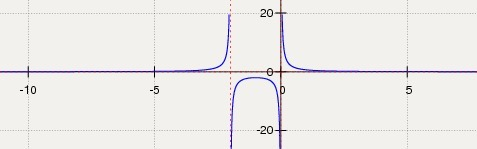
ДАНО
Y = 2/(x² + 2x)
ИССЛЕДОВАНИЕ
1. Область определения.
Х∈(-∞;-2)∪(-2;0)∪(0;+∞)
Разрывы в двух точках.
2. Проверка на четность
Y(-x) = 2/(x² - 2x) ≠ Y(x) - ни чётная ни нечетная.
3. Первая производная.
Y'(x) = -2/[x²*(x+2)] - 2/[x*(x+2)]
4/ Корень производной - точка экстремума - Х= -1.
Экстремум - максимум - Y(-1) = -2
5. Возрастает - Х∈(-∞;-2)∪(-2;-1]
Убывает - X∈[-1,0)∪(0,+∞)
6. Пересечений с осями Х и У - нет. Х∈∅.
7. Наклонная асимптота - Y = 0.
8. Выпуклая - Х∈(-2;0)
Вогнутая - Х∈(-∞,-2)∪(0,+∞)