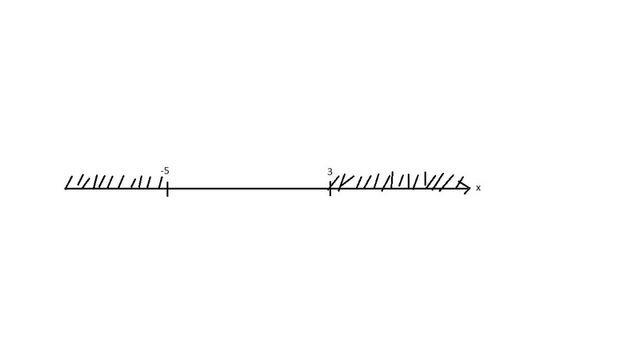Подкоренное выражение больше или равно нулю и знаменатель не равен нулю:

Решим первое неравенство. Сначала найдём корни:
x₁ + x₂ = -2
x₁*x₂ = 15
x₁ = -5
x₂ = 3.
x ∈ (-∞; -5] ∪ [3; + ∞).
Но x ≠ 5.
Тогда x ∈ (-∞; -5) ∪ [3; + ∞).
Ответ: D(y) = (-∞; -5) ∪ [3; + ∞).