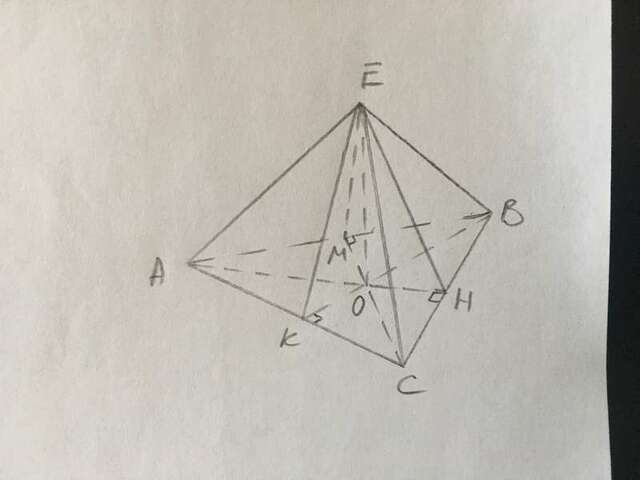
В пирамиде ЕАВС ЕО⊥АВС. ЕК, EM и ЕН - апофемы.
ЕОАВС, ЕО⊥ОК, ЕО⊥ОМ, ЕО⊥ОН, значит по теореме о трёх перпендикулярах ОК⊥АС, ОМ⊥АВ и ОН⊥ВС.
Прямоугольные треугольники ЕКО, ЕМО и ЕНО равны так как ∠ЕКО=∠ЕМО=∠ЕНО и ЕО - общая сторона, значит ОК=ОМ=ОН, значит точко О - центр вписанной в основание окружности.