Отметим на АВ - центр О и соединим О и В с С.
Угол АСВ опирается на диаметр и равен 90°
СD - касательная, перпендикулярна радиусу ОС.
∠ OCD=90°
∠ОСВ+∠ОСА=90°
∠ ACD+OCA=90°
Одни слагаемые этих равных сумм равны, следовательно, и ∠ОСВ=∠ACD
Но ∠ОСВ=∠ОВС ( углы равнобедренного ∆ ВОС)⇒
∠СВD=∠АСD, ч.т.д.
--------
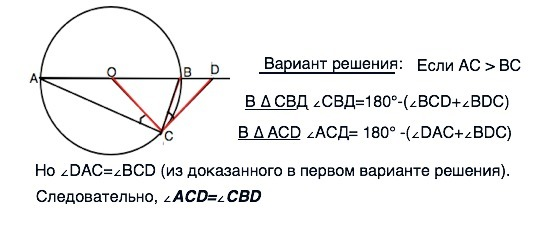
Вариант решения:
Если АС > ВС
В ∆ СВД∠СВД=180°-(∠ВСD+∠ВDС)
В ∆ АСD ∠АСД= 180° -(∠DAC+∠BDC)
Но ∠DАС=∠BCD (из доказанного в первом варианте решения).
Следовательно, ∠ACD=∠CBD