Количество диагоналей N, исходящих из одной вершины многоугольника, находят по формуле:
N = n – 3, где n — число вершин многоугольника..
Для 12-ти угольника N=12-3=9. (См. рисунок приложения)
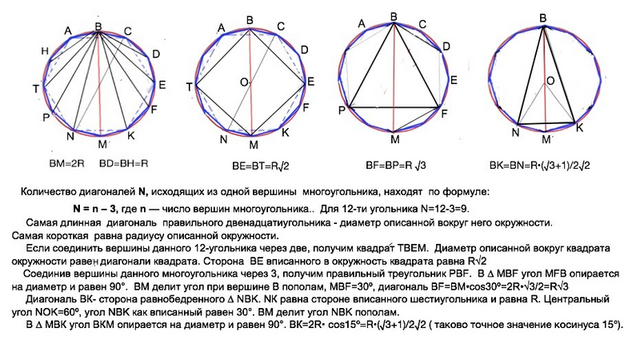
Самая длинная диагональ правильного двенадцатиугольника - диаметр описанной вокруг него окружности.
Самая короткая равна радиусу описанной окружности.
Если соединить вершины данного 12-угольника через две, получим квадрат ТВЕМ. Диаметр описанной вокруг квадрата окружности равен диагонали квадрата. Сторона ВЕ вписанного в окружность квадрата равна R√2
Соединив вершины данного многоугольника через 3, получим правильный треугольник РВF. В ∆ МВF угол MFB опирается на диаметр и равен 90°. BM делит угол при вершине В пополам, МВF=30º, диагональ BF=ВМ•cos30º=2R•√3/2=R√3
Диагональ ВК- сторона равнобедренного ∆ NBK. NК равна стороне вписанного шестиугольника и равна R. Центральный угол NOK=60º, угол NBK как вписанный равен 30°. ВМ делит угол NBK пополам.
В ∆ МВК угол ВКМ опирается на диаметр и равен 90°. ВК=2R•соs15º=R•(√3+1)/2√2 ( таково точное значение косинуса 15°).
Итак, длина диагоналей:
BD=BH=R
BE=BT=R√2
BM=2R
BF=BP=R √3
BK=BN=R•(√3+1)/2√2
--------------
Из условия неясно, 8 см - радиус или длина окружности. Скорее всего, R=8 см. Тогда в найденные длины диагоналей нужно вместо R подставить 8.
Если 8 см=длина окружности, тогда из формулы С=2πR радиус R=4/π