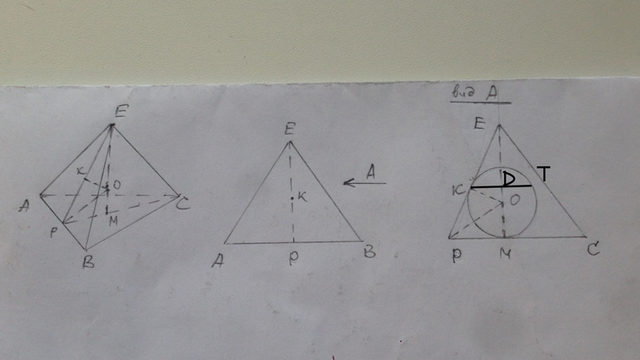
В пирамиду ЕАВС вписан шар. ОК=ОМ=R, ∠ЕРМ=60°.
В тр-ке ЕРМ ОК=ОМ, ОК⊥ЕМ, ОМ⊥РМ, значит РО - биссектриса.
В тр-ке РОМ РМ=ОМ/tg30=R√3.
В тр-ке ЕРМ ЕР=РМ/cos60=2R√3.
Так как грани наклонены к плоскости основания под одним углом, то основание высоты пирамиды лежит в центре вписанной в основание окружности. PM=r.
В правильном тр-ке r=a√3/6 ⇒ a=6r/√3=2r√3.
a=AB=2РМ√3=2R√3·√3=6R.
Площадь боковой поверхности:
Sб=Р·l/2=3AB·EP/2=3·6R·2R√3/2=18R√3 - это ответ.
КТ - диаметр окружности на которой лежат точки касания поверхности шара и боковых граней пирамиды. КТ║АВС.
∠КОМ=∠КОР+∠МОР=60+60=120° ⇒ ∠КОД=180-120=60°.
В прямоугольном тр-ке КДО КД=ОК·sin60=R√3/2.
Длина окружности касания: C=2πr=2π·КД=πR√3 - это ответ.