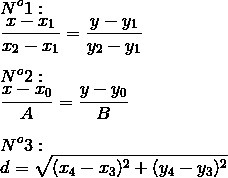Вычислить высоты треугольника, зная координаты его вершин. нужны сами формулы для вставки...

(см. вложение)
Для начала нужно записать уравнения для сторон треугольника. Уравнение прямой, проходящей через две заданные точки - уравнение №1. (x1; y1) и (x2; y2) - координаты точек. После подстановки координат нужно привести уравнение к виду Ax+By+C = 0.
Затем для каждой вершины нужно записать уравнение прямой, проходящей через эту вершину перпендикулярно противоположной стороне - уравнение №2. (x0; y0) - координаты вершины, А и В - коэффициенты из уравнения стороны, на которую опущена высота.
После этого решаем систему из двух уравнений - уравнение высоты и стороны, на которую она опущена. Из этой системы находим x и y, которые являются координатами точки пересечения высоты и стороны.
Теперь, зная координаты двух точек, найдём расстояние между ними по формуле №2, где (x3; y3) и (x4; y4) - координаты точек.

$N^o1:\\\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}\\\\N^o2:\\\frac{x-x_0}{A}=\frac{y-y_0}{B}\\\\N^o3:\\d=\sqrt{(x_4-x_3)^2+(y_4-y_3)^2}$