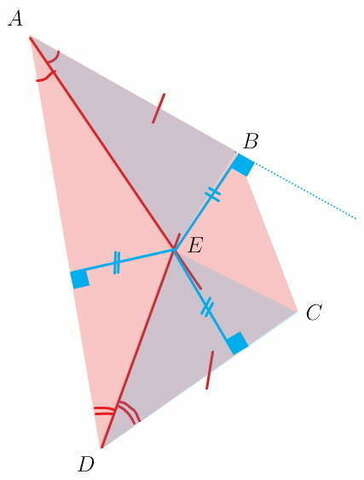
Известно: биссектриса - это ГМТ (Геометрическое Место Точек),
равноудаленных от сторон угла.
т.е. точки, лежащие на отрезке АЕ (любая из этих точек) находятся на одинаковом расстоянии от сторон угла DAB (AE -биссектриса угла DAB),
аналогично, точки, лежащие на отрезке DЕ (любая из этих точек) находятся на одинаковом расстоянии от сторон угла CDA (DE -биссектриса угла CDA), т.е. точка Е одинаково удалена от AB, AD, CD
эти расстояния от точки Е и есть высоты соответствующих треугольников... например, S(ABE) = BE*AB/2
высоты равны, стороны равны (по условию), ---> и площади равны!