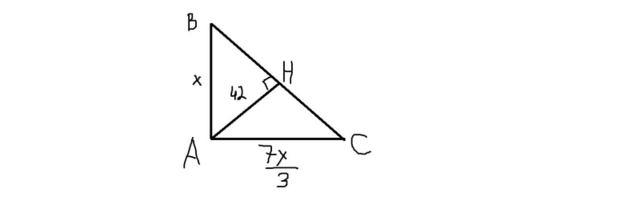
Прежде всего разберемся с обозначениями. Пусть катет AB=x см, тогда, исходя из данного соотношения AB/AC=3/7, AC=(7*AB)/3=(7*x)/3 см. Теперь запишем теорему Пифагора: AB²+AC²=BC², BC=√(x²+(49*x²)/9)=√((58*x²)/9) =√(58)* x / 3 см (x и 3 уже не под корнем, мы извлекли корень из x² и 9). Теперь воспользуемся следующей формулой для нахождения высоты AH=(AB*AC)/BC. AH=42, а катеты и гипотенузы мы выразили через x. Получаем: (7*x²/3)/(√(58)*x/3)=42 (заменим деление умножением, перевернув вторую дробь)→(7*x²/3)*(3/(√58)*x)=42 (3 сокращаются, x тоже)→(7*x)/(√58)=42→x=AB=6*(√58) см, отсюда AC=14*(√58) см. Запишем теорему Пифагора для треугольника AHB: AH²+HB²=AB²→42²+HB²=36*58→1764+HB²=2088→HB²=324→HB=18 см. Запишем теорему Пифагора для треугольника AHC: AH²+HC²=AC²→42²+HC²=196*58→1764+HC²=11368→HC²=9604→HC=98 см. Ответ: гипотенуза делится на отрезки 18 см и 98 см.