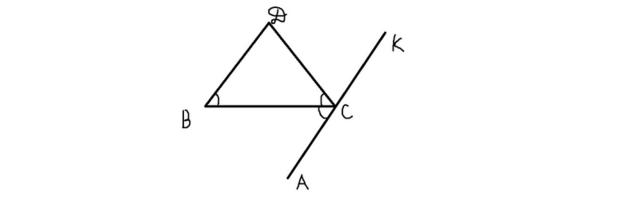
Рассмотрим треугольник BCD. ∠DBC=∠DCB, т.к. треугольник равнобедренный. Так как сумма всех углов треугольника равна 180°, то ∠BDC=180°-2∠DCB. ∠DCB=∠BCA, т.к. по условию BC - биссектриса. Тогда ∠DCK=180°-∠DCB-∠BCA=180°-2∠DCB. Получаем, что накрест лежащие углы при прямых BD и AC и секущей DС равны, а значит BD║AC, что и требовалось доказать.