ДАНО
y=x³-3x²+3x-2
ИССЛЕДОВАНИЕ
1) Область определения - Х∈(-∞;+∞) - непрерывная.
2) Пересечение с осью Х - Х = 2.
3) Пересечение с осью У - У(0) = -2.
4) Поведение на бесконечности
Y(-∞) = - ∞ и Y(+∞) = + ∞
5) Исследование на четность.
Y(-x) = -x³-3x²-3x-2 ≠ Y(x).
Функция ни чётная ни нечётная.
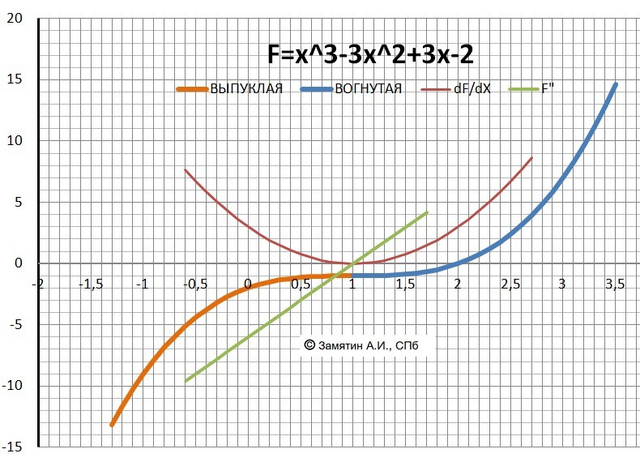
6) Производная функции
Y' = 3x² - 6x + 3
7) Точка экстремума Y' = 0 X = 1
8) Возрастает - Х∈(-∞;+∞)
9) Вторая производная функции
Y" = 6x-6
10) Точка перегиба Y'=0 X=1 - точка перегиба.
11) Выпуклая - Х∈(-∞;1] и вогнутая - X[1;+∞).
12) График прилагается.