1.
а)
ОДЗ: x≠3
Первый корень принадлежит ОДЗ, второй - нет.
Ответ:
x=-2
б)
ОДЗ:
Первый корень не принадлежит ОДЗ, второй - принадлежит
Ответ: x=3
2.
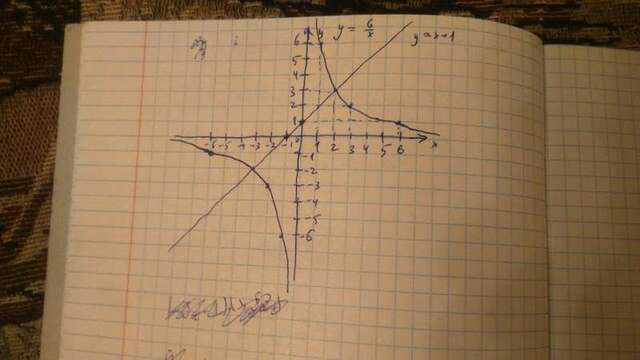
График на фотографии (не так ровно, как хотелось бы, но дальше расписан ход построения).
Как строить:
1)
График функции 
является прямой. Для построения достаточно 2 точек. Ставим : (-1;0), (0,1). Проводим через них прямую.
2)
График функции 
является гиперболой. Асимптоты:
(явным образом видно, что x≠0, y≠0)
Функция нечетная (y(-x)=-y(x)), поэтому достаточно построить для x>0 и отразить относительно начала координат (которое является точкой пересечения асимптот). При 
функция убывает (также выпукла вниз, но, насколько я понимаю, об этом будут рассказывать несколько позже). Ставим несколько точек и строим гиперболу: (1;6), (2;3), (3;2) (6;1). При x стремящемся к 0 и к 
функция стремится к асимптотам (но не пересекает их). Теперь отражаем относительно начала координат и получаем график функции. Смотрим точки пересечения наших двух функций. Получается (2;3) и (-3;-2). Подставляем и проверяем.
Все верно
3.
При движении против течения скорость байдарки относительно берега будет равна разности скорости байдарки в стоячей воде и скорости течения реки. По течению - сумме этих двух величин.
Пусть 
- скорость байдарки, 
- время, что потрачено, когда байдарка плыла по течению и против течения соответственно, тогда по условию:
Второй корень не подходит, так как меньше 0
Ответ: 3 км/ч.
