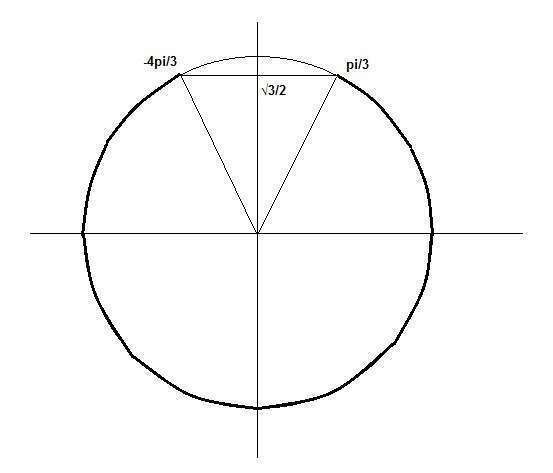
Сначала решим уравнение
sin x/3 = √3/2
Нас здесь не устраивает общее решение:
x/3 = (-1)^n*pi/3 + pi*k
Нам нужно 2 корня с периодом 2pi
x1/3 = 2pi/3+2pi*n = 2pi/3-2pi+2pi*n = ;-4pi/3+2pi*n; x2 = -4pi + 6pi*n
x2/3 = pi/3 + 2pi*n; x1 = pi + 6pi*n
Нас интересует нижняя часть единичного круга, (показано на рисунке) поэтому основное значение x1 должно быть меньше, чем x2.
Теперь решаем наше неравенство:
sin x/3 <= √3/2<br>x ∈ [x1; x2] = [-4pi+6pi*n; pi+6pi*n]