Высота правильной четырехугольной пирамиды равна H, а плоский угол при вершине A. Найдите...

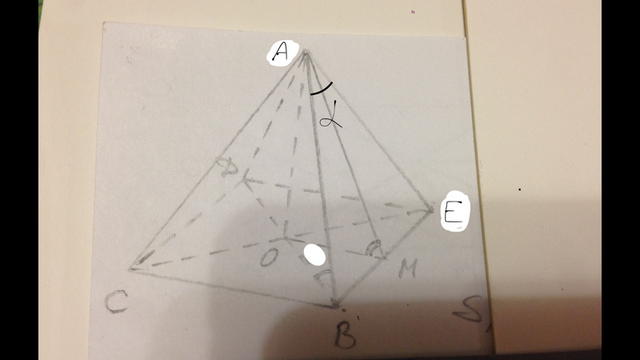
В пирамиде АВСДЕ АО=Н, ∠ВАЕ=α.

Проведём апофему АМ. ВМ=МЕ=ВЕ/2.
Точка О - середина квадрата, значит ОМ=ВЕ/2.
Пусть ВМ=ОМ=х.
В прямоугольном треугольнике АВМ ∠ВАМ=α/2.
АМ=ВМ·ctg(α/2)=x·ctg(α/2).
В прямоугольном тр-ке АМО АО²=АМ²-ОМ²,
Н²=х²·ctg²(α/2)-x²,
x²=H²/(ctg²(α/2)-1).
ВЕ=2ВМ=2х.
Площадь основания: S=ВЕ²=4х²=4Н²/(ctg²(α/2)-1).

Объём пирамиды:
$V= \frac{S*H}{3} = \frac{4 H^{3} }{3( ctg^{2} \frac{ \alpha }{2}-1) }$