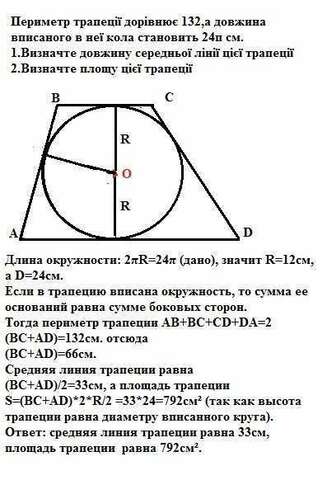
Длина окружности: 2πR=24π (дано), значит R=12см, а D=24см.
Если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
Тогда периметр трапеции АВ+ВС+СD+DA=2(ВС+AD)=132см. отсюда
(ВС+AD)=66см.
Средняя линия трапеции равна
(ВС+AD)/2=33см, а площадь трапеции
S=(ВС+AD)*2*R/2 =33*24=792см² (так как высота трапеции равна диаметру вписанного круга).
Ответ: средняя линия трапеции равна 33см,
площадь трапеции равна 792см².