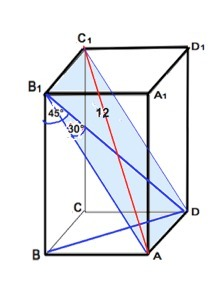
Данный параллелепипед прямоугольный, поэтому все его грани - прямоугольники; противоположные ребра равны и параллельны, боковые ребра перпендикулярны основаниям.
На плоскости основания проекции наклонных АВ1 и DC1 перпендикулярны АD, ⇒ по т. о 3-х перпендикулярах наклонные тоже перпендикулярны AD и В1АDС1- прямоугольник. Его диагонали DB1=АС1=12.
В ∆ ВDВ1 острые углы =45°, он прямоугольный равнобедренный, ВВ1=DB=DB1•sin45°=12•√2/2=6√2
AD=B1D•sin30°=12•0.5=6
АВ=√(BD²-AD²)=√[(6√2)²-6²]=6
Измерения параллелограмма:
AB=6; AD=6, BB1=6√2