ABCD-квадрат со стороной, равной 4 см. Треугольник AMB имеет общую сторону AB с...

Question

ABCD-квадрат со стороной, равной 4 см. Треугольник AMB имеет общую сторону AB с квадратом, AM = BM = два корня из шести. Плоскости треугольника и квадрата взаимно перпендикулярны.
1) Докажите, что BC перпиндикулярно AM.
2) Найдите угол между MC и плоскостью квадрата.
Чертёж обязательно

Answer 1

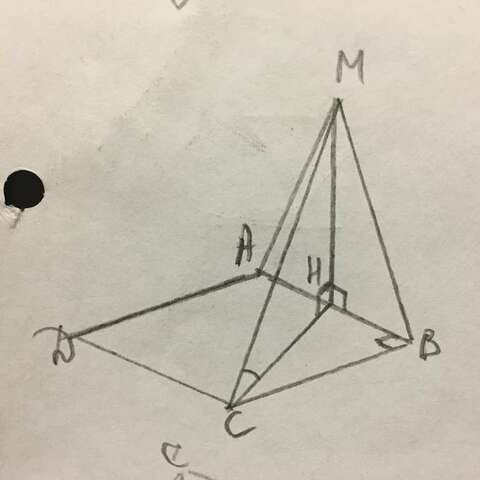
1)  АВС⊥АВМ, ВС∈АВС, ВС⊥АВ ⇒ ВС⊥АВМ.
Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, лежащей в этой плоскости, значит ВС⊥АМ.

2) В равнобедренном треугольнике АВМ проведём высоту МН. АН=ВН=АВ/2=2 см.
В прямоугольном тр-ке СВН СН²=ВС²+ВН²=4²²+2²=20,
СН=2√5 см.
В прямоугольном тр-ке BMH MH²=ВМ²-ВН²=24-4=20,
МН=2√5.
В прямоугольном тр-ке МСН катеты СН и МН равны, значит  ∠МСН=45° - это ответ.

---

Comments

Спасибо большое!

---

Вы бы не могли помочь ещё с одним заданием?

---

Извините, есть ещё вторая часть вопроса: найдите расстояние от А до плоскости DMC. Получается что расстояние это перпендикуляр и он будет равен AD, то есть 4?

---

Нет, немного сложнее. В тр-ке ДМС нужно провести высоту МК_l_СД. В прямоугольном тр-ке МКН нужно провести высоту НР_l_МК. НР - расстояние от прямой АВ до плоскости ДМС. Т.к. АВ ll ДMC, то расстояние от точки А до плоскости ДMC равно НР. В тр-ке МКН по Пифагору найдёте МК. Потом найдёте НР по ф-ле h=ab/c. Всё.

---

Спасибо!