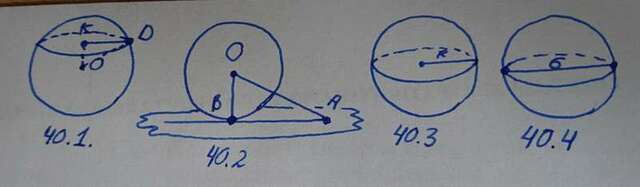
40.1 Пусть точка О - центр шара. Тогда расстояние от центра до сечения равно OK = 3 см.
Сечение шара будет являться окружностью. Пусть радиус сечения равен KD.
KO - расстояние ⇒ KO⊥KD ⇒ ΔKOD - прямоугольный
По теореме Пифагора находим KD:
KD = √(25-9) = √16 = 4 см
S сечения = πR² = πKD² = 16π см²
Ответ: 16π см²
40.2 Пусть О - центр шара. Точка B - точка касания шара и плоскости.
Так как точка А отдалена от пересечения на 4 см, то AB = 4 см.
Расстояние от центра шара до точки касания (OB) равно радиусу шара, то есть половине диаметра.
OB = 6 : 2 = 3 см
OB⊥AB (плоскость касается окружности) ⇒ ΔOAB - прямоугольный
Найдём OA по теореме Пифагора:
OA = √(9+16) = √25 = 5
OA - это радиус шара и расстояние от точки А до поверхности шара.
То есть это расстояние равно AO - OB = 5 - 3 = 2 см
Ответ: 2 см
40.3 S осевого сечения = πR²
4π = R²π
R² = 4
R = 2 см
V шара = 4/3 * π * R³ = 4/3 * π * 8 = 32π/3 см³
Ответ: 32π/3 см³
40.4 Диаметр шара равен 6 см, значит радиус шара равен 6/2 = 3 см
S поверхности шара = 4πR² = 4*9*π = 36π см²
Ответ: 36π см²