S ∆=a•h:2, где а- сторона треугольника, h - высота, проведенная к ней.
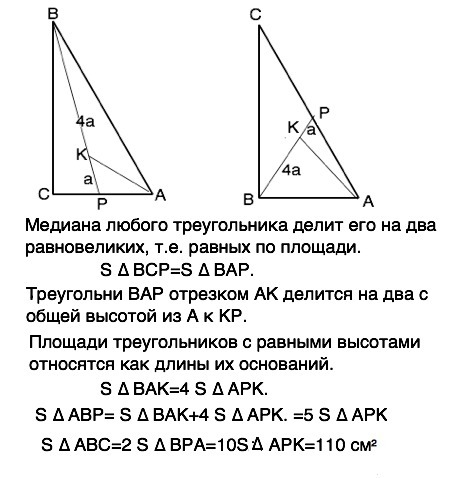
Медиана любого треугольника делит его на два равновеликих, т.е. равных по площади. ( Основания и высоты, проведенные из той же вершины, что медиана, равны).
S ∆ BCP=S ∆ BAP.
Треугольник ВАР отрезком АК делится на два с общей высотой из А к КР.
Площади треугольников с равными высотами относятся как длины их оснований. ⇒
S ∆ BAK=4 S ∆ APK.
S ∆ ABP= S ∆ BAK+4 S ∆ APK. =5 S ∆ APK
S ∆ АВС=2 S ∆ ВРА=10S ∆ АРК=110 см²
-----------
Как видно из приложения, в данном случае ответ не зависит от того, какой угол треугольника равен 90°