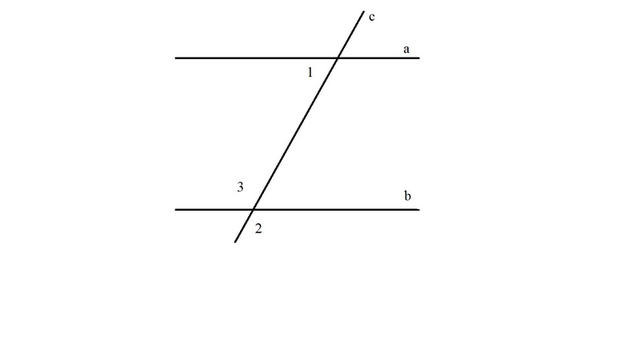№1
Дано: а и в - параллельные прямые; с - секущая, ∠1 = 55*
Найти: ∠2-?
Решение:
Как на рисунке, добавьте ∠3.
∠1 и ∠3 - односторонние => ∠1+∠3 = 180*
∠3 = 180* - 55* = 125*
∠3 и ∠2 - вертикальные => ∠3 = ∠2 = 125*
№2
Дано: две параллельные прямые. ОС - биссектриса, ∠1 = 128*, ∠2 = 52*
Доказать: АО=АС
Найти: ∠АСО
Решение:
Р/м ∠1 и ∠АОВ. По свойству ∠1+∠АОВ = 180*
∠АОВ = 180* - 128* = 52*
Т.к ОС - биссектриса => ∠АОС=∠СОВ=1/2∠АОВ = 26*
∠СОВ и ∠АСО - накрестлежащие, поэтому они равны ∠АСО = 26*
____
Р/м треугольник АСО. ∠АОС=26*, ∠АСО = 26* следовательно ∠АОС=∠АСО = 26* следовательно это равнобедренный треугольник, боковые стороны которого равны, т.е. АО=АС