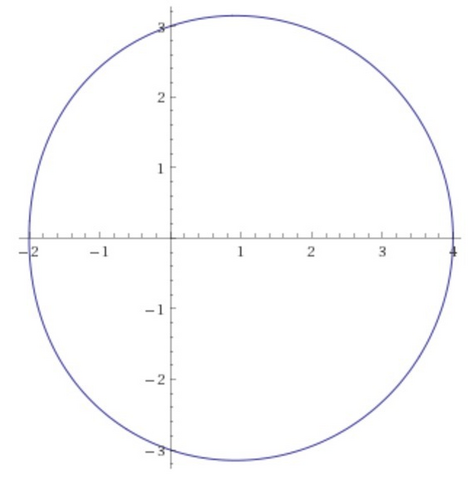
График во вложении.
Площадь под кривой равна интегралу:

(интеграл от 9 равен 9 * 2π, интеграл от косинуса по периоду равен 0, интеграл от (sin^2 phi + cos^2 phi) равен 2pi, а интеграл только от cos^2 phi равен половине от 2pi)
Достаточно правдоподобный результат, учитывая, что фигура близка к окружности радиуса 3 с центром в точке (1, 0).