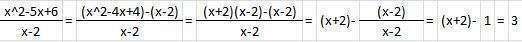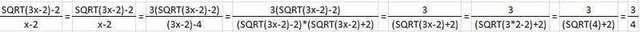Решение первого во вложении.
2) f=(x^3)/3 + (x^2)/2 - 2x - 5;
Чтобы найти экстремумы, надо взять первую производную и приравнять её к нулю.
f'=x^2+x-2;
x^2+x-2=0; (находим корни, они и есть точки экстремумов)
D=1+8=9;
x1=(-1+3)/2=1;
x2=(-1-3)/2=-2;
Чтобы проверить, какой экстремум является максимумом, а какой минимумом, надо взять вторую производную в точках экстремума и посмотреть на её знак. Если она больше нуля, то это минимум, если меньше, то это максимум.
f''=2x+1;
f''(x1)=2*1+1=3 (3>0, значит в точке x=1 минимум функции)
f''(x2)=2*(-2)+1=-3 (-3<0<span>, значит в точке x=-2 максимум функции)
P.S. минимумы и максимумы могут быть локальными!!!