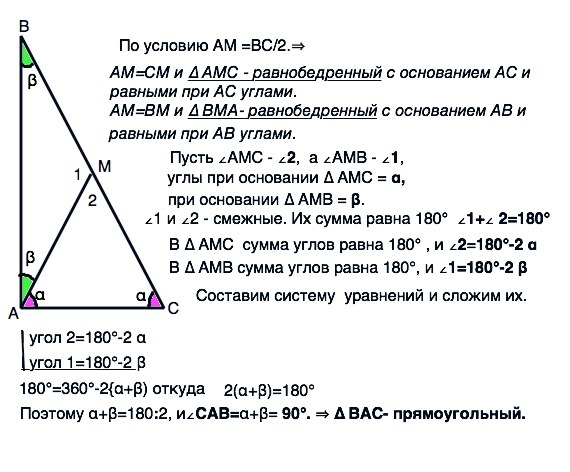
По условию медиана АМ треугольника АВС равна 1/2 стороны ВС.
Тогда АМ=СМ и ∆ АМС - равнобедренный с основанием АС и равными при АС углами.
АМ=ВМ, и ∆ ВМА равнобедренный с основанием АВ и равными при АВ углами.
Обозначим угол АМС - ∠2, угол АМВ - ∠1, углы при основании ∆ АМС - α
при основании ∆ АМВ - β.
∠1 и ∠2 - смежные. Их сумма равна 180°
∠1+∠ 2=180°
В ∆ АМС сумма углов равна 180° , и
∠2=180°-2 α
В ∆ АМВ сумма углов равна 180°, и
∠1=180°-2 β
Составим систему уравнений и сложим их.
| угол 2=180°-2 α
| угол 1=180°-2 β
180°=360°-2{α+β) откуда
2(α+β)=180°
Поэтому α+β=180:2, и∠САВ=α+β=90°. ⇒ ∆ ВАС- прямоугольный.