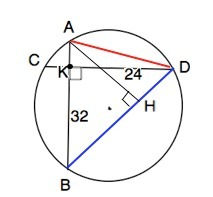
a)При пересечении двух хорд окружности получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды. (теорема).
СK•KD=AK•KB
CK=AK•KB:KD=6•32:24=8 см
CD=8+24=32 см
AB=6+32=38 см
б) По т.Пифагора BD=√(BK²+DK²)=√1600=40
sin∠КBD=KD:BD=24/40=0,6
Расстояние от точки до прямой - длина перпендикулярного отрезка. AH ⊥ BD;
AH=AB•sinABD=38•0,6=22,8 см
в) Из ∆ AKD гипотенуза AD=√(AK*+KD*)=√(36+576)=6√17
∆ABD вписанный. По т.синусов:
AD:sinABD=2R
R=0,5•(6√17):0,6=5√17