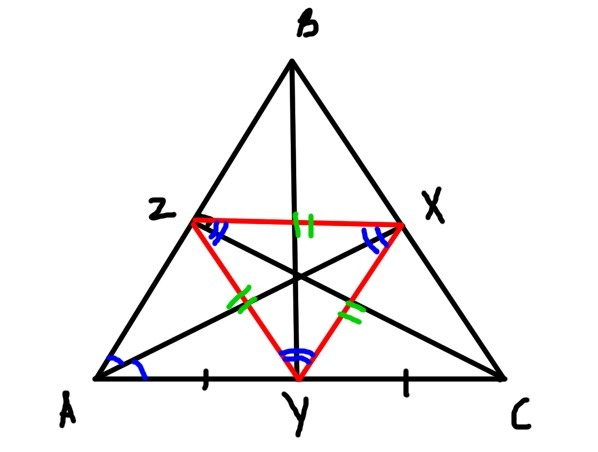
Рассмотрим прямоугольный треугольник AZC
ZY- медиана прямоугольного треугольника проведённая к гипотенузе , значит ZY=AY=YC
Так как треугольник XYZ равносторонний , то стороны YX и XZ тоже равны половине стороны АС
XY=YZ=ZX=AY=YC
Значит треугольник AXC тоже прямоугольный. Так как медиана проведённая к большей из его сторон равна половине этой стороны.
Значит АX - высота, но AX и биссектриса , а это значит, что треугольник АВС является равнобедренным . Также АX может быть медианой, а это значит что ВХ=ХС
ZX- медиана прямоугольного треугольника BZC (CZ⊥AB по условию)
Значит ZX=BX=XC, ZX=XY=YZ=YC=YA=AY=YB ⇒ AB=BC=CA