3.
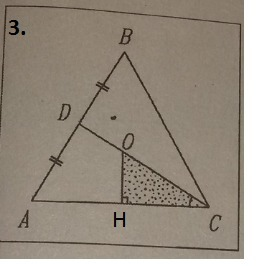
1) Расстояние от точки О до прямой АС - длина перпендикуляра, обозначим основание перпендикуляра буквой Н.
Тогда ΔОНС - прямоугольный, ОН=4 см, ∠ОСН=30°, катет ОН, лежащий напротив угла 30° равен половине гипотенузы, значит ОС - гипотенуза равна 4*2=8 см.
2) По условию задачи точка О - точка пересечения медиан ΔАВС, а медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины, значит
OC/OD=2/1;
8/OD=2/1;
OD=8*1/2=8/2=4 (см).
Ответ: 4 см.
4.
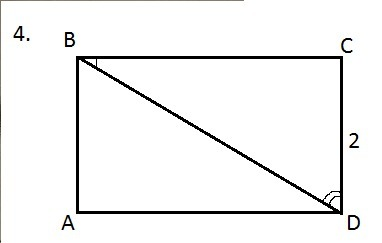
1) Пусть ABCD - прямоугольник, CD=2 см. Из площади прямоугольника можно вычислить сторону ВС= 4√3/2=2√3 (см).
2) Рассмотрим ΔBCD - прямоугольный, BC и CD - катеты,
tg∠CBD=CD/BC=2/(2√3)=√3/3, ⇒∠CBD=30°;
∠BDC=90°-30°=60°.
Ответ: 30°, 60°.
5.
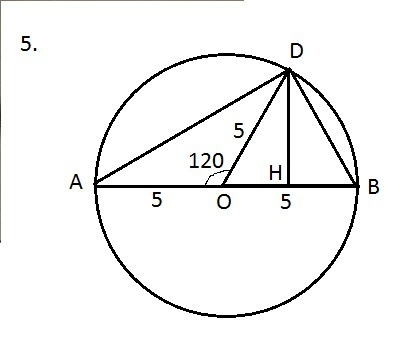
1) ΔADB - прямоугольный, так как ∠OAD=∠ODA=(180°-120°)/2=30°,
∠DOB=∠OBD=∠ODB=60°, ⇒∠ADB=180°-(30°+60°)=180°-90°=90°.
2) S(ADB)=1/2*AD*DB;
AB=10 см, DB=1/2*AB=1/2*10=5 (см),
по т.Пифагора AD=√(AB²-DB²)=√(10²-5²)=√(100-25)=√75=5√3 (см).
S(ADB)=1/2*AD*DB=1/2*5√3*5=25√3/2 (см²).
3) ΔODB - равносторонний, расстояние от точки D до АВ - длина перпендикуляра DH. Высоту равностороннего треугольника можно вычислить по формуле DH=OB√3/2=5√3/2 (см).
Ответ: 25√3/2 см²; 5√3/2 см.