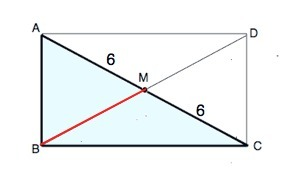
Обозначим треугольник АВС, угол В=90°. ВМ - медиана, ⇒АМ=СМ=6.
Достроим треугольник до прямоугольника ABCD. Проведем диагональ ВD. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Точка М - середина АС, она же делит диагональ ВD пополам. Половины диагоналей прямоугольника равны.
⇒ВМ=АМ=СМ=6 (ед. длины)
-----------
Запомним это полезное свойство: Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.