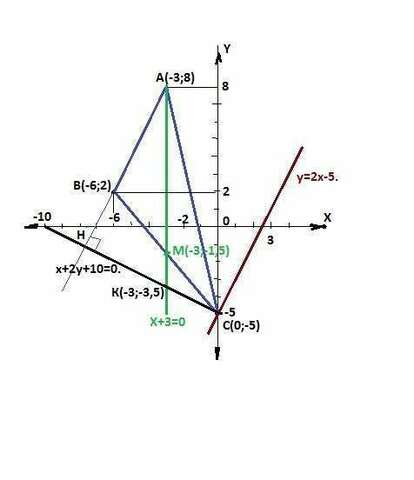
Даны вершины треугольника (ABC):A(-3,8)B(-6,2),C(0,-5)
а)Найти стороны AB, ВС и АС.
Решение:
Модуль или длина вектора: |ab|=√((Xb-Xa)²+(Yb-Ya)²).
В нашем случае
|АВ|=√((-6-(-3))²+(2-8)²)=√((-3)²+(-6)²)=√45=3√5.
|АC|=√((0-(-3))²+(-5-8)²)=√(3²+(-13)²)=√178.
|BC|=√((0-(-6))²+(-5-2)²)=√(6²+(-7)²)=√85.
б)Уравнение высоты CH
Уравнение прямой, проходящей через точки А и В:
(X-Xa)/(Xb-Xa)=(Y-Ya)/(Yb-Ya) =>
(X+3)/(-3)=(Y-8)/(-6), отсюда
2X-Y+14=0 (1) - Общее уравнение прямой Аx+Вy+С=0, где в нашем случае
А=2, В=-1 и С=14.
Из уравнения прямой АВ (1) «снимаем» вектор нормали: n(2;-1), который и будет
направляющим вектором прямой CH.
Уравнение прямой СH составим по точке С(0;-5) и направляющему вектору n(2;-1):
(x-0)/2=(y-(-5))/-1 или x+2y+10=0.
в)Уровнение медианы AM
Координаты середины М стороны ВС:
М(Xb+Xc)/2;(Yb+Yc)/2) или М(-3;-1,5)
Уравнение прямой, проходящей через точки А и М:
(X-Xa)/(Xm-Xa)=(Y-Ya)/(Ym-Ya) =>
(X+3)/0=(Y-8)/(-9,5), отсюда
X+3=0
г)Точку пересечения медианы AM и высоты CH
Точку пересечения двух прямых найдем, решив систему двух уравнений:
x+2y+10=0 и X+3=0 методом подстановки Х=-3.
-3+2y+10=0 или y=-3,5.
Координаты точки пересечения Р(-3;-3,5)
д)Уравнение прямой,проходящей через вершину С параллельно стороне AB
Уравнение прямой, проходящей через точки А и В:
2X-Y+14=0 (1) - найдено выше. Его можно представить в виде:
y=2x+14.
Прямая, проходящая через точку С(Хс;Yc) и параллельная прямой y=ax+b,
представляется уравнением y-Yc=a*(x-Xc).
В нашем случае а=2.
Искомое уравнение: y+5=2x-0 или y=2x-5.
е)Расстояние от точки С до прямой AB.
Это высота из точки СН, найденная в п.б.